| [ Information ] [ Publications ] [Signal processing codes] [ Signal & Image Links ] | |
| [ Main blog: A fortunate hive ] [ Blog: Information CLAde ] [ Personal links ] | |
| [ SIVA Conferences ] [ Other conference links ] [ Journal rankings ] | |
| [ Tutorial on 2D wavelets ] [ WITS: Where is the starlet? ] | |
If you cannot find anything more, look for something else (Bridget Fountain) |
|
|
|
|
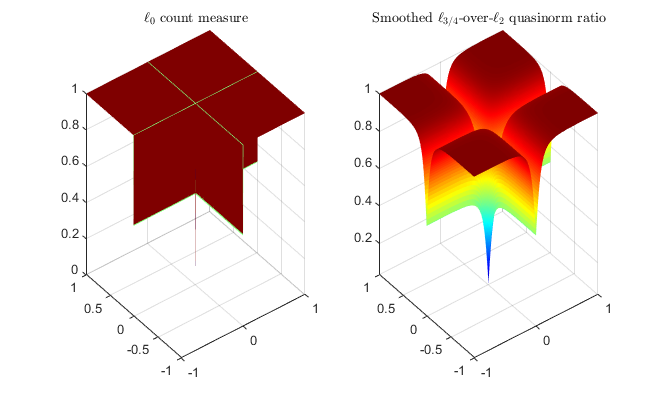
Sparsity-promoting data restoration/recovery with SPOQ smooth/non-convex penalty with quasi-norm/norm ratios to emulate the "sparse" l0 count measure

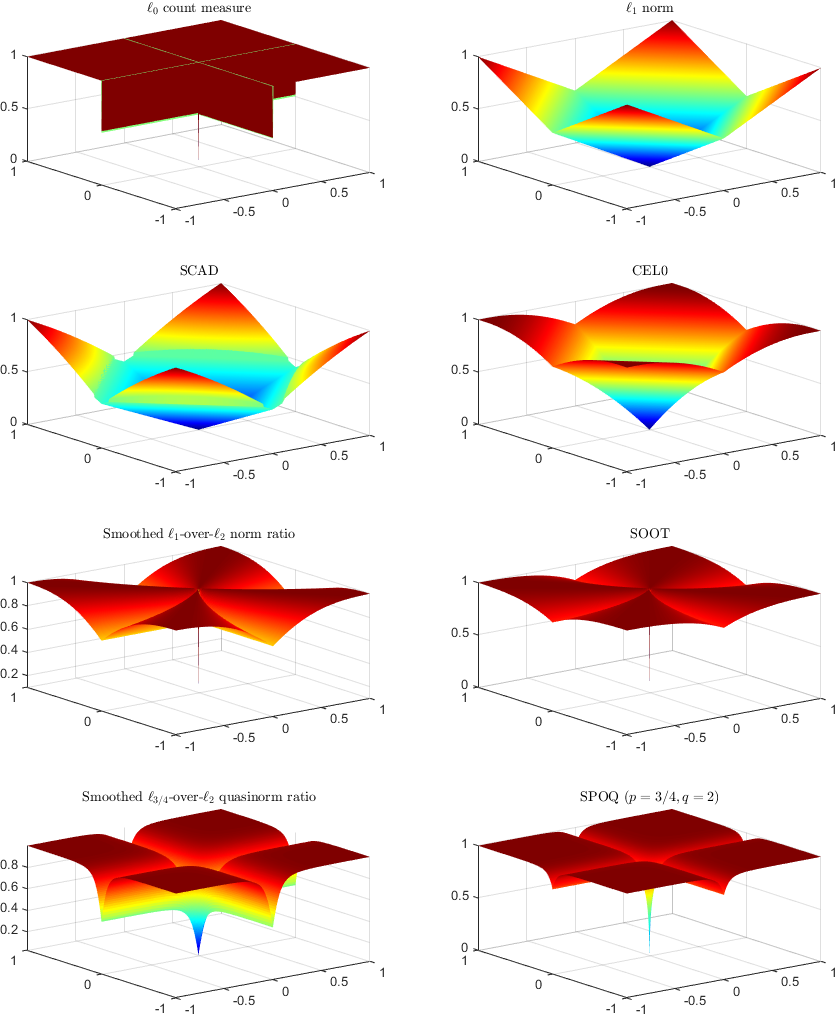
Abstract: Underdetermined or ill-posed inverse problems require additional information for sound solutions with tractable optimization algorithms. Sparsity yields consequent heuristics to that matter, with numerous applications in signal restoration, image recovery, or machine learning. Since the l0 count measure is barely tractable, many statistical or learning approaches have invested in computable proxies, such as the l1 norm. However, the latter does not exhibit the desirable property of scale invariance for sparse data. Extending the SOOT Euclidean/Taxicab l1-over-l2 norm-ratio initially introduced for blind deconvolution, we propose SPOQ, a family of smoothed (approximately) scale-invariant penalty functions. It consists of a Lipschitz-differentiable surrogate for lp-over-lq quasi-norm/norm ratios with p in ]0,2[ and q>=2. This surrogate is embedded into a novel majorize-minimize trust-region approach, generalizing the variable metric forward-backward algorithm. For naturally sparse mass-spectrometry signals, we show that SPOQ significantly outperforms l0, l1, Cauchy, Welsch, SCAD and CEL0 penalties on several performance measures. Guidelines on SPOQ hyperparameters tuning are also provided, suggesting simple data-driven choices.
The law of parsimony (or Occam's razor, named after William of Ockham, stated as "Entities should not be multiplied without necessity", "Non sunt multiplicanda entia sine necessitate") is an important heuristic principleand a guideline in history, social and empirical sciences. In modern terms, a preference to simpler models, when they possess - on observed phenomena - a power of explanation comparable to more complex ones. In statistical data processing, it can limit the degrees of freedom for parametric models, reduce a search space, define stopping criteria, bound filter support, simplify signals or images with meaningful structures. For processes that inherently generate sparse information (spiking neurons, chemical sensing), degraded by smoothing kernels and noise, sparsity may provide a quantitative target on restored data. On partial observations, it becomes a means to selecting one solution, among all potential solutions that are consistent with observations.